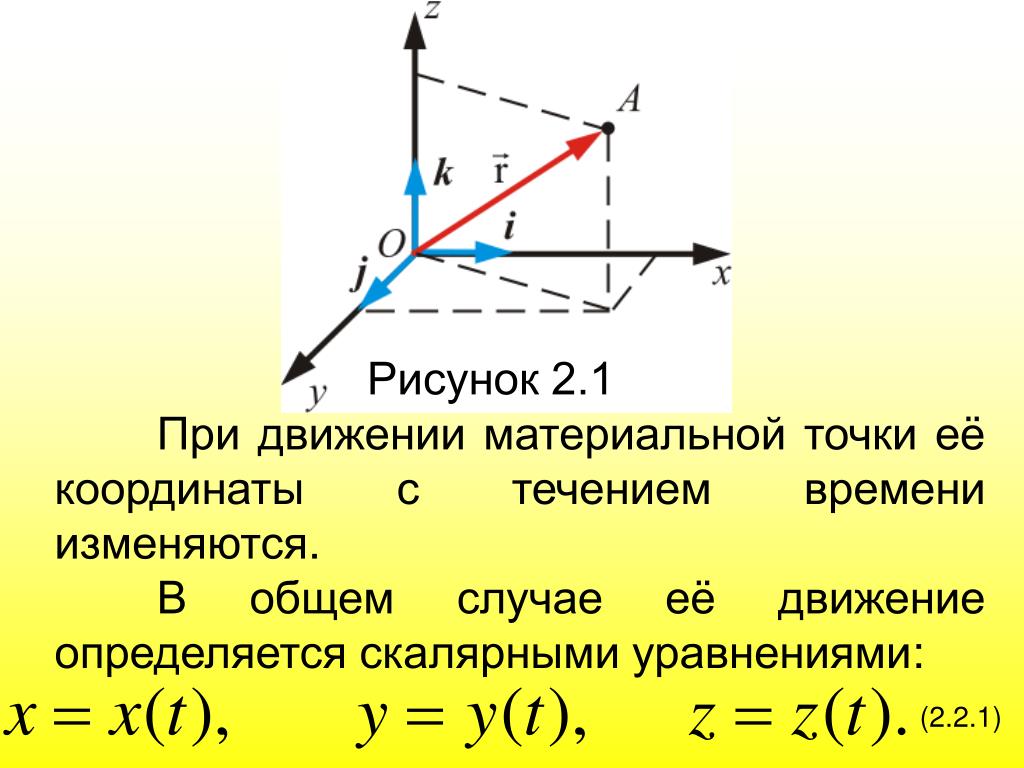
Движение материальной точки — одно из основных понятий физики, изучающее перемещение объекта в пространстве относительно времени. В своей простейшей форме точку можно представить как объект, не имеющий размеров и массы. Математическое описание движения точки обычно осуществляется с помощью таких величин, как позиция, скорость и ускорение.
В данной статье рассмотрим движение материальной точки по закону x(t) = t2 — 9t + 22. Здесь x(t) — функция, описывающая позицию точки в зависимости от времени t. Подставляя различные значения времени, мы можем получить соответствующие координаты точки в пространстве.
Важно отметить, что закон движения x(t) = t2 — 9t + 22 представляет собой квадратичную функцию, что означает, что изменение координаты точки происходит нелинейно, а с изменением времени траектория движения может приобретать различные формы.
Подобное движение может быть интересно изучать, так как позволяет представить различные ситуации, в которых точка может перемещаться в пространстве. Знание законов движения и умение анализировать и предсказывать траекторию точки является основой в таких областях, как физика, инженерия и астрономия.
Физическая модель движения материальной точки
Физическая модель движения материальной точки позволяет изучать ее перемещение во времени и пространстве. В данном случае, функция x(t) описывает зависимость координаты точки от времени. Параметры в этом уравнении, такие как коэффициенты перед t^2, t и свободный член, определяют форму и скорость движения точки.
Зная уравнение движения, можно получить такие важные параметры, как скорость и ускорение точки. Скорость v(t) определяется производной по времени от функции x(t), а ускорение a(t) — второй производной:
v(t) = d/dt(x(t))
a(t) = d^2/dt^2(x(t))
Таким образом, физическая модель движения материальной точки позволяет не только описать ее координаты в пространстве, но и изучить изменение скорости и ускорения во времени. Это дает возможность более глубокого понимания физических законов, управляющих движением объектов в механике.
Таким образом, физическая модель движения материальной точки на основе заданного закона x(t) позволяет исследовать основные параметры движения и его характеристики. Это является важным инструментом анализа и построения прогнозов в механике и других областях, где изучается движение объектов.
Математическое описание движения
Закон движения x(t) = t2 — 9t + 22 задает положение точки на оси x в каждый момент времени t. Здесь t представляет собой время, а x(t) — положение точки в данный момент времени.
Первый член уравнения t2 представляет квадрат времени, который описывает изменение положения точки с течением времени, второй член -9t учитывает линейное изменение положения со временем, а третий член 22 представляет начальное положение точки.
Математическое описание движения позволяет предсказывать положение точки в любой момент времени и анализировать ее движение. Например, можно вычислить скорость и ускорение точки, а также определить точку, где она достигнет максимальной или минимальной координаты.
Таким образом, закон движения x(t) = t2 — 9t + 22 предоставляет математическую модель для описания движения материальной точки, и его анализ может дать много информации о движении и свойствах точки в разные моменты времени.
Формула закона движения
Формула закона движения представляет собой квадратное уравнение, где t представляет время. В данном случае, формула представляет движение точки в одномерном пространстве. Зная значение времени, мы можем расчитать позицию точки на оси координат.
Выражение t^2 означает квадрат времени, а выражение -9t представляет перемещение точки со скоростью -9 единиц по оси координат. Константа 22 представляет начальную позицию точки в момент времени t = 0.
Используя формулу закона движения, мы можем рассчитать позицию точки в любой момент времени и изучать ее движение в пространстве. Также можно производить анализ скорости и ускорения точки посредством дифференцирования формулы движения.
Численные значения коэффициентов в формуле
В данной формуле:
Коэффициент при t2: 1
Коэффициент при t: -9
Свободный член: 22
Эти численные значения являются ключевыми составляющими для определения зависимости положения точки от времени. Они позволяют точно вычислить положение точки в любой момент времени и понять направление ее движения.
Интерпретация коэффициентов
- Коэффициент при t^2: значение этого коэффициента равно 1. Он отражает квадратичный характер движения, указывая на то, что функция x(t) имеет параболическую форму.
- Коэффициент при t: значение этого коэффициента равно -9. Он показывает скорость движения точки в начальный момент времени, а именно -9 единиц длины в соответствующей системе измерения в единицу времени. Его отрицательное значение указывает на то, что точка движется влево.
- Свободный член: значение этого коэффициента равно 22. Он представляет собой начальное положение точки в момент времени t = 0. То есть, в начальный момент времени, точка находится на расстоянии 22 единиц длины от начала координат.
Таким образом, анализируя коэффициенты уравнения движения, мы можем получить информацию о форме траектории, начальной скорости и начальном положении материальной точки.
Графическое представление движения
Для этого на оси абсцисс откладываются значения времени (t), а на оси ординат – соответствующие им значения координаты (x).
Используя уравнение движения, можно легко определить координаты точек на графике.
Найдем первую точку:
подставим t = 0 в уравнение x(t):
x(0) = (0)2 — 9(0) + 22 = 22
Таким образом, первая точка на графике будет иметь координаты (0, 22).
Аналогично, найдем вторую точку:
подставим t = 1 в уравнение x(t):
x(1) = (1)2 — 9(1) + 22 = 14
Вторая точка на графике будет иметь координаты (1, 14).
Аналогично можно найти и другие точки, соответствующие различным значениям времени. Подходящий масштаб и соответствующая интерпретация осей позволят получить полное представление о движении материальной точки.
Построение графика зависимости координаты от времени
График будет представлять собой кривую, которая отражает изменение положения точки в пространстве в зависимости от времени.
Для построения графика необходимо выбрать значения времени (t) и вычислить соответствующие значения координаты (x) с помощью заданной формулы.
Полученные данные можно представить в виде точек на координатной плоскости, где по оси абсцисс откладывается время (t), а по оси ординат — координата (x).
Соединив все полученные точки линией, можно получить график зависимости координаты от времени, который позволяет визуально оценить изменение положения материальной точки во времени.
Определение момента времени, когда положение точки не меняется
Для определения момента времени, когда положение точки не меняется, необходимо найти значения времени, при которых производная функции положения точки равна нулю. Производная функции положения точки показывает скорость изменения положения точки во времени.
Используя заданный закон движения материальной точки x(t) = t^2 — 9t + 22, можем найти производную этой функции. Для этого применяем правило дифференцирования степенной функции и правило дифференцирования суммы функций:
x'(t) = 2t — 9
Приравниваем производную к нулю и решаем уравнение:
2t — 9 = 0
Отсюда получаем, что
t = 4.5
Таким образом, в момент времени 4.5 положение точки не меняется.
Вопрос-ответ:
Какой закон движения материальной точки в статье?
Закон движения материальной точки в статье задан выражением: x(t) = t^2 — 9t + 22.
Какие значения принимает функция x(t)?
Функция x(t) принимает значения, которые можно получить, подставив конкретные значения t в выражение x(t) = t^2 — 9t + 22.
Каков физический смысл функции x(t) = t^2 — 9t + 22?
Функция x(t) = t^2 — 9t + 22 описывает положение материальной точки в зависимости от времени. Здесь x — координата точки, t — время. Таким образом, функция показывает, как меняется положение точки с течением времени.
Как можно использовать закон x(t) = t^2 — 9t + 22 в практических применениях?
Закон x(t) = t^2 — 9t + 22 может быть использован для моделирования и анализа движения материальных точек. Например, он может быть полезен при изучении движения тел в физике, расчете траектории объектов в инженерии или прогнозировании положения объектов в задачах геодезии.